Path Integral Molecular Dynamics
Talk at CECAM Flagship School of Path Integral Quantum Mechanics
Classical molecular dynamics (MD) simulations are very powerful in describing physical and chemical processes at the molecular level, following the dynamics in time of each individual particle. However, at low temperatures and/or for light particles (Hydrogen and Helium are prominent examples) a classical description is inadequate. Quantum simulations are much more difficult to perform than classical simulations. In fact, their computational cost scales exponentially with the number of particles.
Can we have the cake and eat it too? Quantum simulations at a classical cost.
It would be ideal if we could have the computational efficiency of classical MD simulations but describe quantum mechanical effects. It turns out that this is possible! The path integral (PI) formulation of quantum mechanics shows that the partition function of a quantum particle is identical to that of a classical ring polymer composed of P replicas of the original particles connected with harmonic springs. Exact quantum expectation values are obtained when P is increased until convergence. So we can use classical MD simulations to study thermodynamics of quantum systems!

PIMD for indistinguishable particles
Now you know that PIMD simulations are a very useful tool for studying thermodynamics of quantum condensed phases. However, they also have several limitations. In our group we develop new methods to push the boundaries of PIMD simulations. One of the major ones is that they completely neglect the fact that quantum particles are bosons or fermions, one of their most fundamental properties! We have developed a new algorithm to perform PIMD simulations for bosons and fermions. How does it work? Take two particles, for example: If they are indistinguishable particles, their wave function has to be symmetric/anti-symmetric with respect to permutation of the particles. In PIMD this means that instead of considering one ring polymer for each particle, as shown above, you need to also consider one long ring polymer composed of the two particles connected together, shown below.
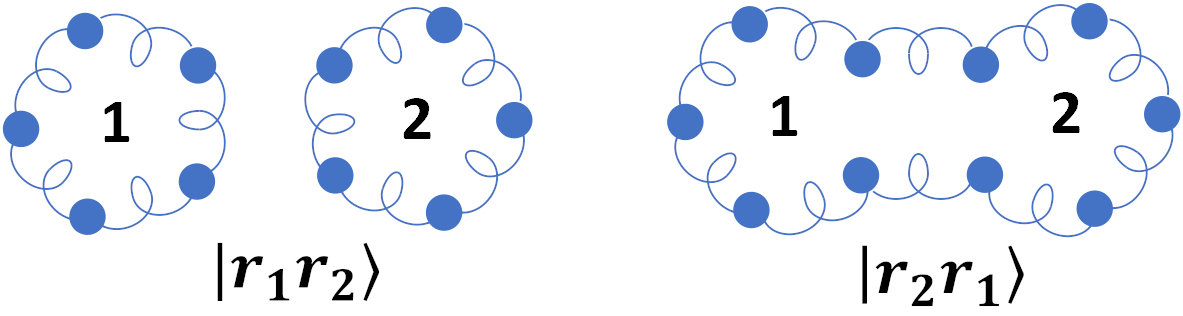
However, the main problem is that the number of ring polymers configurations you need to consider for more than two particles scales exponentially with system size. Because of this, it was not possible to perform PIMD simulations of bosons and fermions for more than very few particles. We have shown that the forces and potential required for PIMD simulations of indistinguishable particles can be evaluated recursively, which reduced the computational cost from exponential to cubic and enabled the first simulations of large bosonic systems using PIMD. We have also shown that the same simulations can be used to obtain expectation values also for fermions using reweighting. However, the simulations for fermions suffer from very poor convergence at low temperatures. This is an important problem called the fermion sign problem. We showed that by using a simple free-energy inequality it is possible to alleviate this problem at simulate systems at much lower temperatures than otherwise possible.
Relevant publications:


.png)